Orientation

General Description

Given in Quaternions
- qw as Scalar Quaternion
- qx as X-Rotation Quaternion
- qy as Y-Rotation Quaternion
- qz as Z-Rotation Quaternion
Hamilton Convention
Right-Handed System
Rotates from Inertial Frame (on Tag) to World Frame (East-North-Up)

Inertial Frame

The original Coordinate System of the Tag.

📘
The Inertial Coordiante System is always the same on the Tag, regardless how the Tagis oriented in the Enviroment.

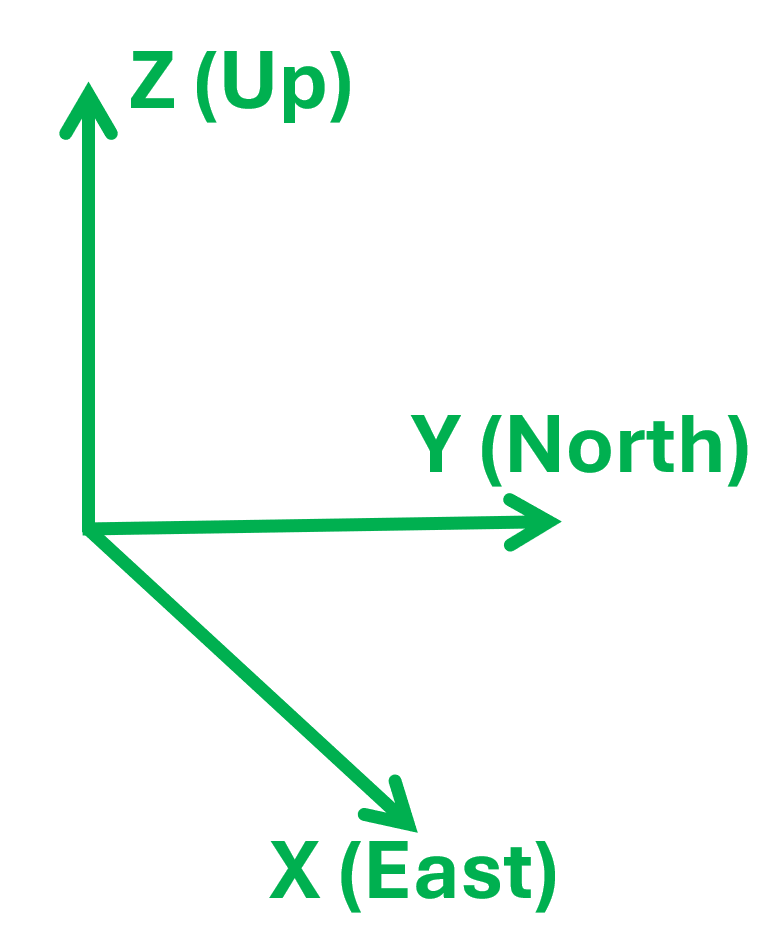
World Frame

The World Coordinate System aligned with the Magnetic North

East-North-Up (ENU) Convention
X is aligned with East
Y is aligned with the North
Z is aligned with the height

📘
The 3D Model must always be aligned with the Magnetic North. Therfore, the World Coordinate System is equal to the Coordinate System of the 3D Model.

Rotation with Quaternions

Assume a Vector V_Inertial shall be rotated from the Inertial Frame (on Tag) to the World Frame (East-North-Up) V_World.
The Vector V_Inertial consists of Vx_Inertial, Vy_Inertial and Vz_Inertial.

The Vector V_World consists of Vx_World, Vy_World and Vz_World.

    Vx_World = Vx_Inertial * (1 - 2 * (qy^2 + qz^2)) + Vy_Inertial * 2 * (qx * qy - qw * qz) + Vz_Inertial * 2 * (qw * qy + qx * qz);
    Vy_World = Vx_Inertial * 2 * (qx * qy + qw * qz) + Vy_Inertial * (1 - 2 * (qx^2 + qz^2)) + Vz_Inertial * 2 * (-qw * qx + qy * qz);
    Vz_World = Vx_Inertial * 2 * (-qw * qy + qx * qz) + Vy_Inertial * 2 * (qw * qx + qy * qz) + Vz_Inertial * (1 - 2 * (qx^2 + qy^2));

📘
There are several ways to rotate a 3D Vector. We provided above a closed-form solution, where the Quaternions are converted to a Roation Matrix, which is multiplied with the previous Vector.

📘
The Formulas above can always be used for Quaternions with the Right-Handed and Hamilton Convention

Right-Handed Quaternion Conversion to Left-Handed Quaternion

Some external Software Solutions use Left-Handed Quaternion Convention
Therefore, the Right-Handed Hamilton Quaternions from the API have to be converted to the Left-Handed Hamilton System:
- Exchange the Z with the Y Quaternion
- Negate the X, Y and Z Quaternion

qw_LeftHanded = qw;
qx_LeftHanded = -qx;
qy_LeftHanded = -qz;
qz_LeftHanded = -qy;

📘
This was just an example for the Conversion to Left-Handed Systems. Different external Software Solution may have different Orientation Conventions. The Orientation Conventions between the API (Hamilton, Right-Handed) must match with the external Software Solution's Convention. Otherwise the results are wrong.

Acceleration

General Description

Given in 3D in m/s^2
Inertial Acceleration:
- Data from Sensor
- Scaled and Bias compensated
- axInertial as the Acceleration in the inertial X-Direction
- ayInertial as the Acceleration in the inertial Y-Direction
- azInertial as the Acceleration in the inertial Z-Direction
World Acceleration:
- Rotation from Inertial Frame to World Frame already applied
- Scaled, Bias compensated, Low-Pass and High-Pass filtered
- axWorld as the Acceleration in the East-Direction
- ayWorld as the Acceleration in the North-Direction
- azWorld as the Acceleration in the Up-Direction

📘
The World Acceleration from the API is already rotated towards East-North-Down and preprocessed (Bias, Noise and Drift compensated) and can be used without further adjustments required.

Acceleration Conversion to Left-Handed Coordinate System

Some external Software Solutions require Left-Handed Coordinate Systems
Therefore, the Right-Handed Coordinate System from the API has to be converted to the Left-Handed Coordinate System:
- Exchange the Z with the Y Acceleration

axWorld_LeftHanded = axWorld;
ayWorld_LeftHanded = axWorld;
azWorld_LeftHanded = ayWorld;

📘
This was just an example for the Conversion to a Left-Handed Coordinate System. Different external Software Solution may have different Coordiante System Conventions. The Coordiante System Conventions between the API (Right-Handed) must match with the external Software Solution's Convention. Otherwise the results are wrong.